
本日は2問です。学び直しで頭を活性化します
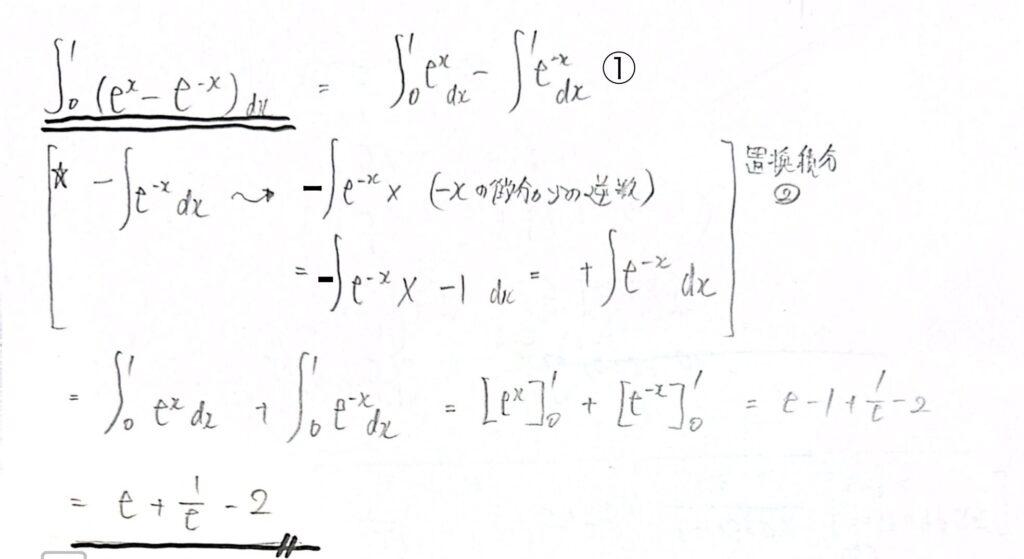
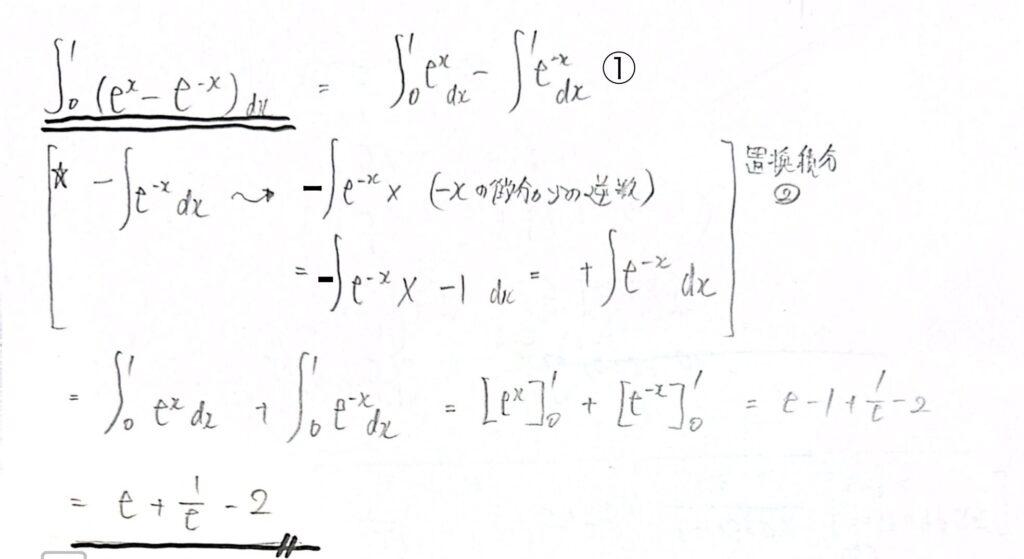


問1 指数関数(置換積分利用)の定積分
こちらの問題は”指数関数”に注意する問題です。
ネイピア数”e”が出てくる段階で少々構えてしまう私です。
けれど”ネイピア数”よりまずは”指数関数”の積分で尚且つ指数に”-”が付いている。
その事に注意が必要です。
この”指数関数”の置換積分をついつい忘れてしまいます。
要するに置換積分の”微分して逆数”の件です。
②で”微分して逆数”を忘れずに掛けましょう。
すると+∫eの-x乗が出てきます。
ここまで来たら後は簡単です。
丁寧に計算してミスがないように注意しましょう。
問2 部分分数分解を含んだ定積分
思考
こちらの問題まずは”むむ、部分分数分解か?”と気付けるかどうかがスタートになります。
”被積分関数”がそもそも積になっているのでまずやりにくいな。。なんて感じると思います。
更に分数だし。なんて辺りでなんとなーく部分分数分解が気になっていきます。
部分分数分解
私この部分分数分解は結構好きです。
この前の加法定理は苦手なんですが。
忘れそうな時は分数の”通分”を思い出せば大丈夫です。なにを隠そう部分分数分解は通分の逆の作業です。
”通分”は分数の足し算において分母がそれぞれ違う時分母を公倍数で統一する事で足し算を行う方法です。
言い換えると和を積で表現しているとも言えるのでこれを大いに利用して積を和に変える事で積分をやりやすくする。そんなテクニックです。
しかしこの”通分”って小学校低学年で習いましたよね?
その延長を高校になってから勉強するのってなんか凄いな。と思うのは私だけでしょうか?
個人的に思うに通分を教わったこの”通分”を教わった時に部分分数分解もついでに教えたほうが効率が良いような気がします。
という事で③で閃いて部分分数分解へ進みます。
恒等式
なぜ部分分数分解が好きなのかというとこの”恒等式”が好きなんです。
”恒等式”ってなんとも数学らしくないですかね?
④で通分から逆の作業をする際に出てきた方程式を利用して連立方程式へ進み”a”と”b”を求めます。
⑤でa,bに代入する事で⑥へと整理します。
⑦で積分の性質を利用して計算ミスをなくします。
log
最終までひと踏ん張りです。
それぞれ被積分関数がxについて分数になっているので回答はlogになりそうです。
⑦~⑧の行程で各項積分しますがこの際の注意点は
そうです。積分した後のlogに”絶対値”が付くことです。
この1/xが積分する事でlogになる行程が怪しい人は復習しましょう。
もし絶対値が怪しい人は絶対値の復習をしましょう。→自分の事です。。。
この絶対値がつく事に注意して後は足し算です。
⑨の行程で忘れがちなlogの底と真数が同じ時一つの括りで考える事なんかも注意です。
慣れれば感覚で理解できるのですが数学から離れた学び直し勢はあれ?どうするんだっけ?と結構なります。
丁寧に計算して⑩から回答となります。
























