
タイトルは一問ですが実際は二問です。では本日も学び直し始めましょう。
第一問
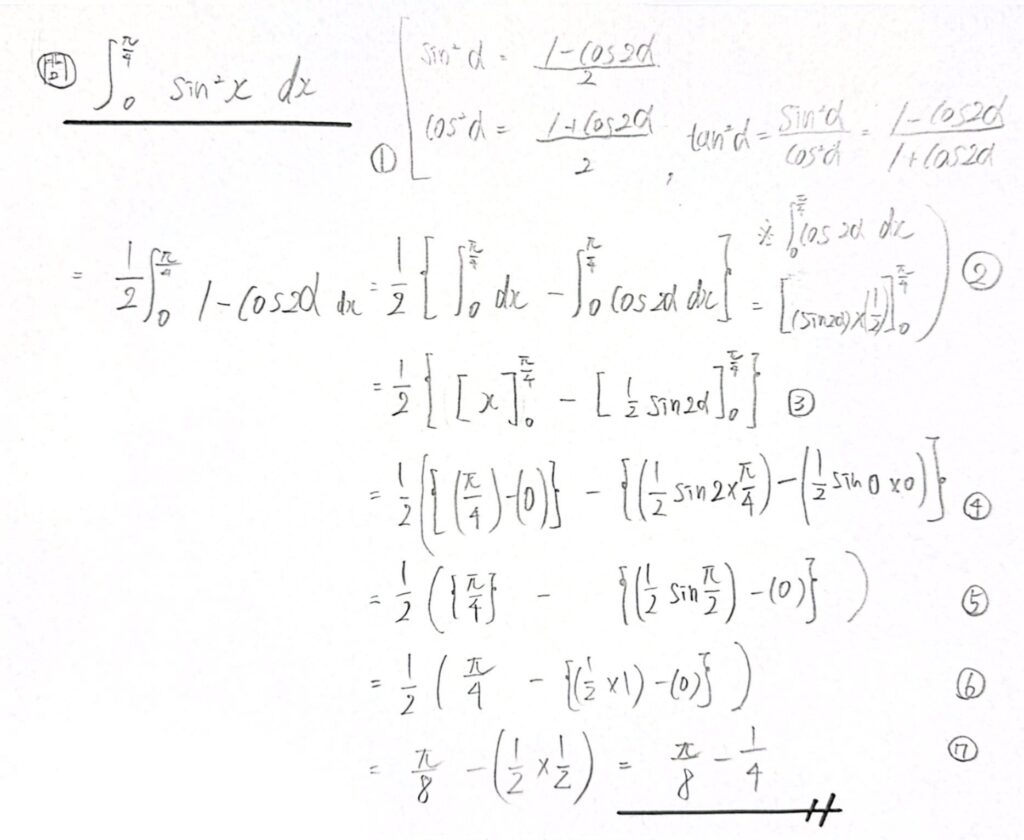
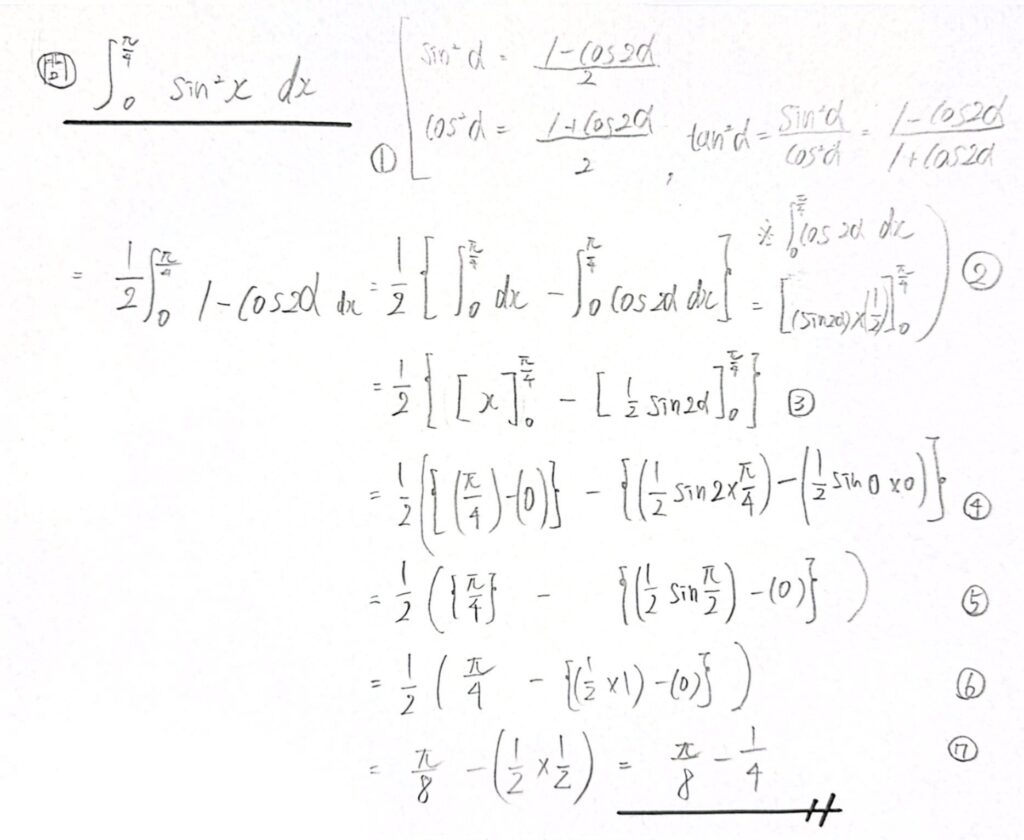
”加法定理”からの”次数下げ”問題
この手の問題はかなり慣れてきました。
加法定理を利用して”次数を下げる問題”です。
この公式をすぐ思い出せる自分なりの方法で見つける事が大事です。
今だとネットに覚え方が沢山出ています。
自分なりの方法をぜひとも見つけましょう。
受験生は大体5秒で思い出せるようにした方がいいそうですね。
私はすぐ忘れちゃうんですけどね。。。
ここを雑に計算すると全てが水の泡になってしまいます。
丁寧に計算ミスに注意しましょう。
第二問
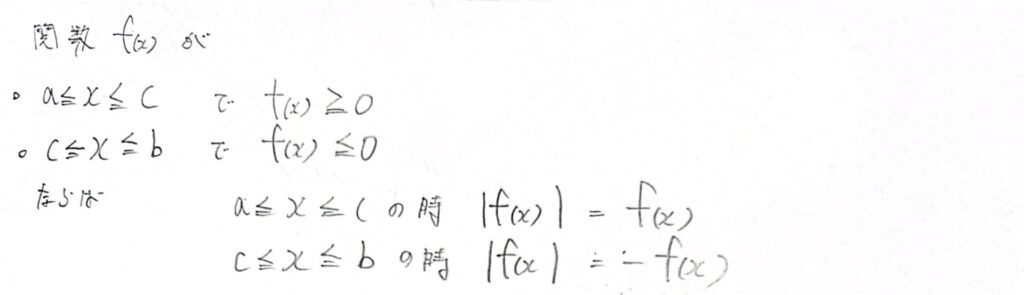
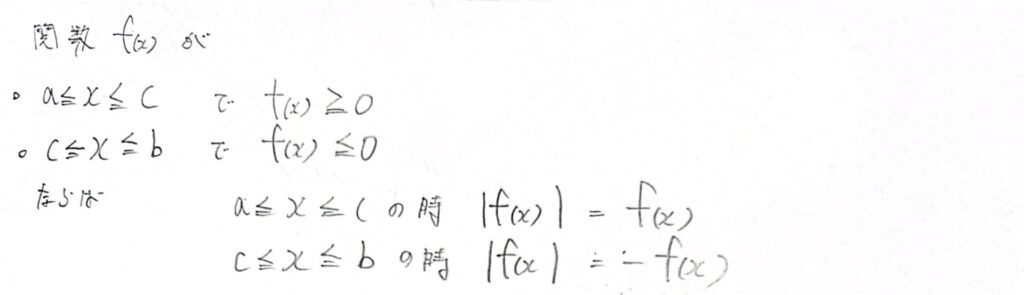


”絶対値のついた関数”の定積分
絶対値。
嫌いな人は嫌いですよね。
自分も嫌いでした。。。
ちなみに自分が少し絶対値を理解できるようになったのは”存在している”、”大きさ”、”量”などの目に見える”プラス”の概念が整理出来るようになって頭に入ってきた気がします。
今回の様な絶対値の問題は言語化すると問題が解きやすい気がするので言語してみます。
問題の言語化
この問題は”定積分”です。つまり数字が回答になります。
そしてその”定義域”は上端と下端に表されています。
すなわち”πからπ/3″です。
”絶対値”で被積分関数が表記されています。
この範囲内で”y”がプラスになる定積分と”y”が-を表す範囲は-をかける事でプラスにして”定積分”を求めてください。
という問題です。
”絶対値関数”のポイント
切り替わるポイントを見つける事。
これが”絶対値”関連の問題を解く”カギ”です。
ここではつまり”y”が”0”になる”x”を発見する事です。
①がそのポイントで関数”cos x”が”0”を表すのが”π/2″です。
そして与えられている”範囲の条件”と照らし合わせれば②と③が導き出せます。
そして③の範囲は”y”が”-”を表すので”-f(x)”にすることで”絶対値”の条件を満たします。
その後は積分計算
残りの計算はただの積分計算になります。
積分計算 sin→-cos→-sin→cos→sin
まとめ



”絶対値”の”概念と理解”が出来ていればさほど難しい問題ではないですね。
後はとにかく丁寧に計算ミスがないようすれば問題ない思います。
いかがでしたか?今回は
”次数下げの問題”と”絶対値のついた関数”でした。
参考になれば幸いです。
























