本日は学び直しの数学で頭を活性化。思考の訓練していきましょう。
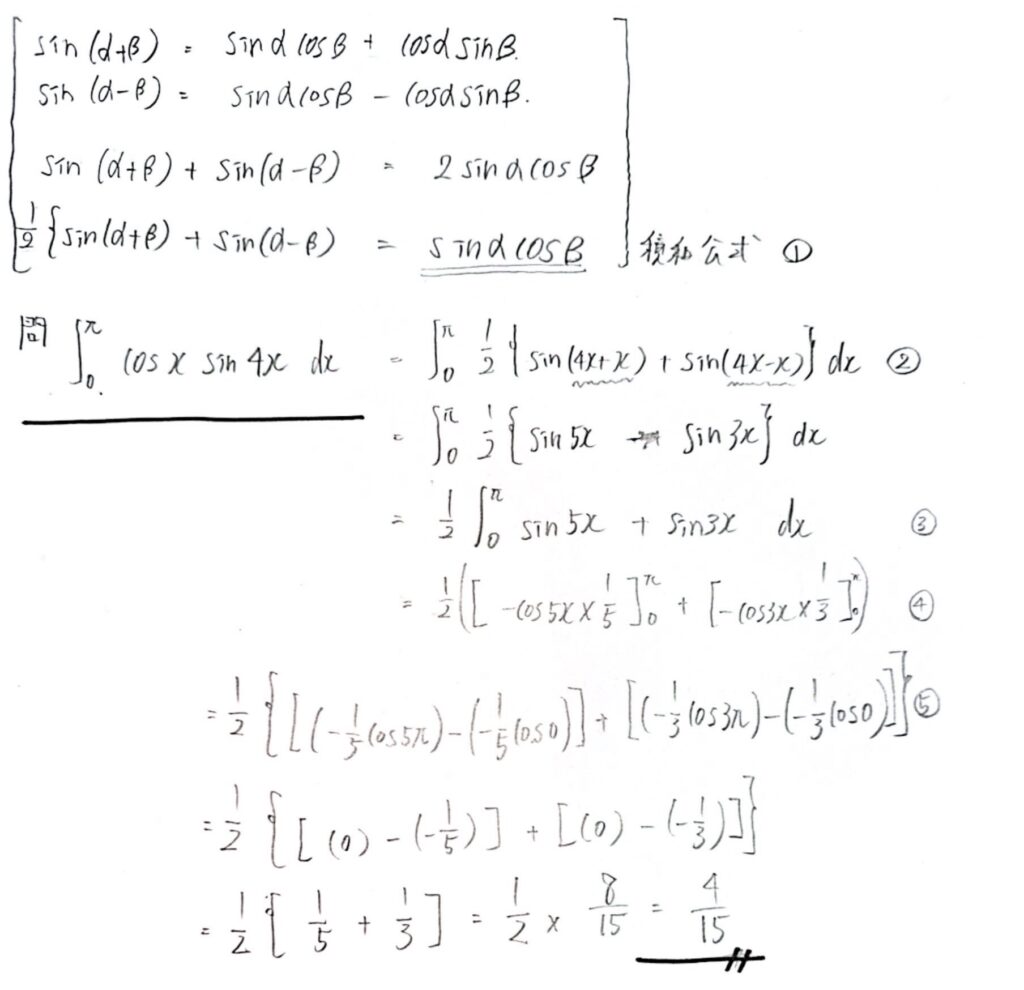
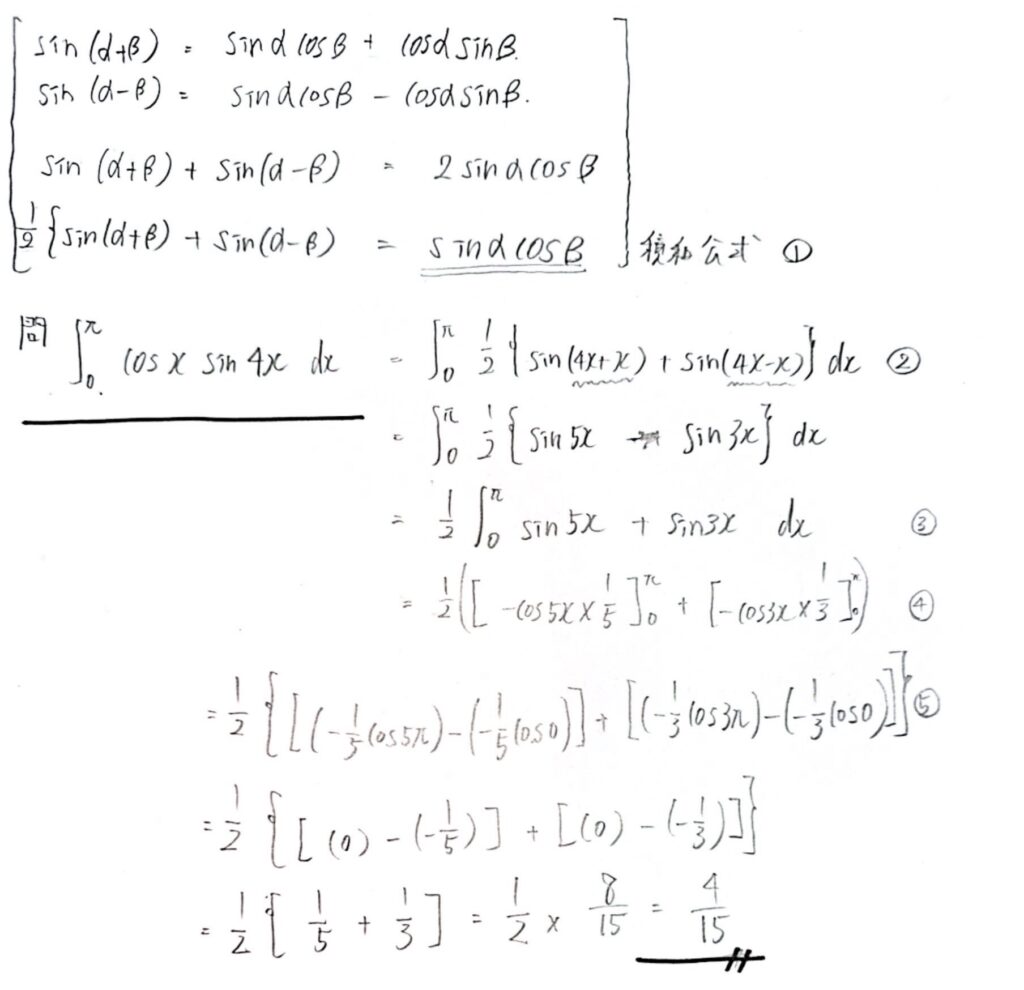
目次
”積和公式”を利用した定積分
- ・まずは数Ⅱで習った積和公式を利用します。
-
ピンとくるかがポイントですが”被積分関数”が”積の形”は気持ち悪いです。
大体いつもこの違和感ですね。
なのでいかに”項”の形へ変形できるかがポイントと考えました。
- ・積和公式忘れた時
-
絶対に覚えなければならないサイタコスモスコスモスサイタ。
積和公式は”加法の形”を”積の形”に変形できる事が特徴です。
なので①のように”積の形”を一つ残す作業をしてあげれば完成します。
①でよく間違うのがsin同士を同類項のように扱うミスです。
あくまでαとβは角度であるので同類項のようには扱えないので注意しましょう。
- ・αとβは４xでもｘでもどっちでもよい（計算しやすい方に合わせる）
-
②において積和公式の形にした際、今回のケースではαが”４ｘ”でβが”ｘ”の方が公式に代入した時計算が楽です。
公式が”sinαcosβ”だからですね。
なので問題に合わせ臨機応変にαとβを決めてください。
- ・③で積分の性質を利用して整理
- ・④で積分します。
-
外側積分×内側逆数
- ・定積分の計算を丁寧に行う
-
④~⑤にかけて丁寧な計算を心がけましょう。
三角関数の知識が必要ですが普通に落ち着いて考えれば難しくはないはずです。
符号にも注意です。
以上です。
まとめ
積和公式を導く事が出来さえすれば現役の方々には基本中の基本の問題かと思います。
いかがでしたか？積和公式を利用した定積分の問題でした。
参考になれば幸いです。
¥1,587 （2024/11/15 17:05時点 | 楽天市場調べ）
ポチップ
