
今回の学び直しの一問は数学Ⅱで扱った三角関数の単元を利用した問題です。
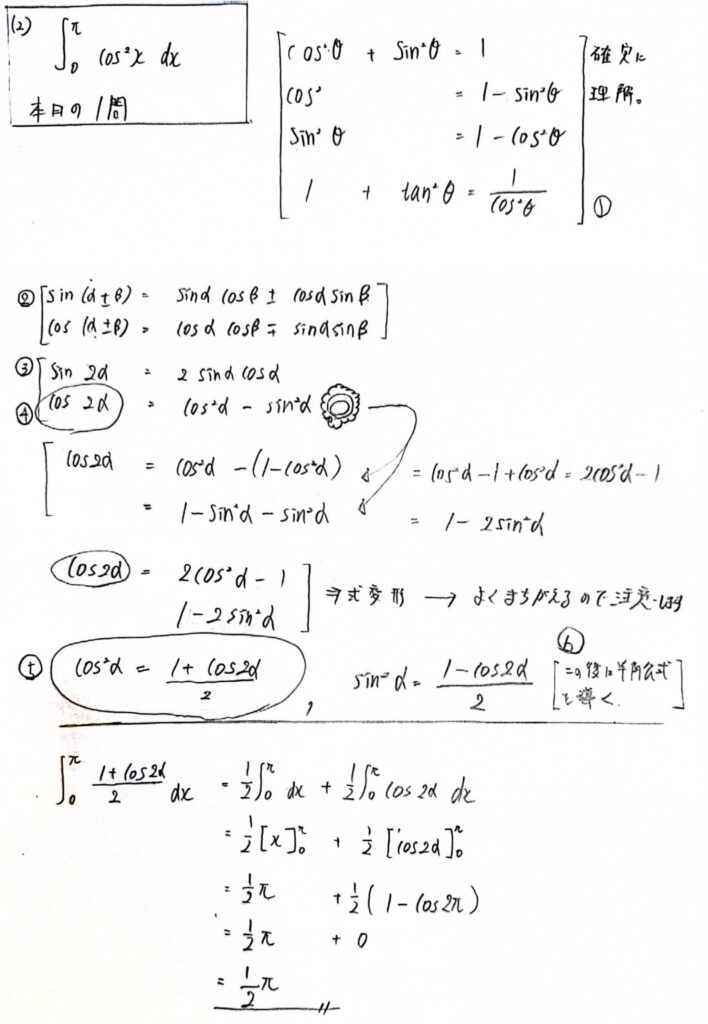

思考の全体像
〇こちらの問題を見た時に解きにくさを感じると思います。
被積分関数が三角比の二乗。
すなわち三角比が積の形になっています。
〇基本的に我々に与えらる問題は被積分関数が一次式の形である事が多いので二乗でましてや三角比だと解きにくい訳ですね。
〇簡単にするために数Ⅱで習った加法定理から色々な公式へ式変形する際に三角関数の次数を下げる事ができたな。
そしてその事を問われているのだな。と気付けるか?が全てだと思います。
〇その点に気付ければ数学Ⅱの知識で解けてしまうという問題です。
数Ⅱ復習/加法定理応用/次数下げ
〇次数下げの問題かな?と気付いたところでそれを思い出すのが大変なんですけどね。私の場合。。。
〇大変ですが忘れたら1から思い出します。
〇まずは数Ⅰの三角比からです。①の公式ですがこれは何があっても忘れられないし意味さえしっかり理解できれば忘れようがありません。
もしこの①があやふやな方は一度数Ⅰに戻って確実に理解しましょう。
理解出来れば時間がかかっても解ける問題です。
〇次に②の加法定理へすすみます。
これは例の念仏です。(サイタコスモス、コスモスサイタ&コスモスコスモス、サカナイサカナイ)
〇③は応用で2倍角の公式ですね。
角度αが同じになるのでsinの2倍角はsinαcosαが二倍、cosの2倍角は二乗になりますね。
〇このうちcos2αに関しては更に式変形していく事を数Ⅱで教わりました。
〇④に①の公式を代入してcos2αを2通り作ります。そしてこちらの一方を利用します。
- そして今回のポイントとなるのがこの④です。左辺はcos2αで一次式なのですが右辺に二次式を発見できます。
- つまり④を利用すれば三角関数の二次式を三角関数の一次式にする事ができる。
- 今回の問題のような被積分関数が三角関数で二次式の時に三角関数の一次式にできる。
- すなわち次数を下げる事ができる。という発見でもあります。
〇数Ⅱでは半角公式を出す際の途中式としてさらっと触れていますがこの途中式を大いに利用します。
〇ちなみにわたしはここで移項する際によく間違えて時間ロスします。。。慌てず丁寧に計算しましょう。
〇二次式を一次式にする公式といえます。完成したのが⑤
〇数Ⅱではここから半角公式を導きます。
不定積分の計算を丁寧すれば終了
〇三角関数が一次式になったので後は丁寧に計算するだけなので簡単です。
〇分数になっているという事は1/2が項に掛けられている事と同じですから積分計算の基本性質から∫の前に1/2をもっていきます。
〇これ当たり前っぽいし省略しちゃう時がありますが1/2を前にもって行く事で計算ミスが減りますので(私の場合だけかもしれませんが)丁寧に計算しましょう。
いかがでしたか?本日は加法定理を応用した、次数下げの問題を扱ってみました。



ほとんど数Ⅱの復習加法定理周辺の問題でした。しかし時間が経つと忘れやすいし面倒くださいので忘れた時にどーするか?を私の場合は意識しています。
























